
The procedure works by comparing the variance between group means versus the variance within groups as a way of determining whether the groups are all part of one larger population or separate populations with different characteristics. The name "analysis of variance" is based on the approach in which the procedure uses variances to determine whether the means are different. For more detailed information about the differences between specific means, use a multiple comparison method such as Tukey's. If the p-value is less than your alpha, then you conclude that at least one durability mean is different. Because you are examining one factor (carpet type) you use a one-way ANOVA. You put a sample of each carpet type in ten homes and you measure durability after 60 days. Transformations of the original dataset may correct these violations.įor example, you design an experiment to assess the durability of four experimental carpet products. However, ANOVA procedures work quite well even if the normality assumption has been violated, unless one or more of the distributions are highly skewed or if the variances are quite different. ANOVAs require data from approximately normally distributed populations with equal variances between factor levels. To perform an ANOVA, you must have a continuous response variable and at least one categorical factor with two or more levels. (All Minitab command names are written in capitals in these notes, for clarity, but in actual use they can. At its simplest (there are extensions) ANOVA tests the following. The null hypothesis states that all population means (factor level means) are equal while the alternative hypothesis states that at least one is different. Two commands are used for anovas: ANOVA and ANCOVA. The null hypothesis states that all population means (factor level means) are equal while. Be sure to select from the drop-down in the. To run the ANOVA, we use the sequence of tool-bar tabs: Stat > ANOVA > One-way. Because it is an inferential technique, any two-way ANOVA is actually concerned with the set of m values that correspond to the sample means that are computed from study’s data. The data ( Lesson1 Data) can be copied and pasted from a word processor into a worksheet in Minitab: Step 2: Run the ANOVA. Like any one-way ANOVA, a two-way ANOVA focuses on group means. ANOVAs assess the importance of one or more factors by comparing the response variable means at the different factor levels. ANOVA (i.e., two independent variables with a minimum of two levels each). A sample of the 5-step classical method for this example is on the page following the Session Window page. Analysis of variance (ANOVA) tests the hypothesis that the means of two or more populations are equal. When you do the assignment for this lesson you will turn in the printed Session Window and the paper with the hypothesis testing procedure written out. ANOVAs assess the importance of one or more factors by comparing the response variable means at the different factor levels. write in the ANOVA table using the results from Minitab, but use the format from our text.
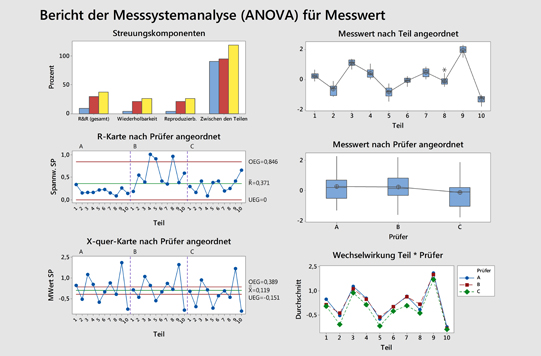
Analysis of variance (ANOVA) tests the hypothesis that the means of two or more populations are equal.


 0 kommentar(er)
0 kommentar(er)
